NLP 04 - RNN을 개선한 LSTM과 GRU 모델
BoostCamp AI Tech
NLP
Natural Language Processing
RNN
LSTM
GRU
02/16/2021
본 정리 내용은 Naver BoostCamp AI Tech의 edwith에서 학습한 내용을 정리한 것입니다.
사실과 다른 부분이 있거나, 수정이 필요한 사항은 댓글로 남겨주세요.
LSTM & GRU
LSTM
Long Short-Term Memory(LSTM)은 기존 RNN모델에서 Vanishing/Exploding Gradient 문제를 해결하고, long-term depandancy 문제를 개선한 모델이다.
hidden state를 단기(short-term)기억소자로 볼 수 있고, 보다 먼 timestep(long-term)의 정보까지 잘 반영하도록 만들었기 때문에 이러한 이름이 붙었다.
구조
기존의 RNN 모델이 다음과 같은 형태였다면,
LSTM 모델의 형태는 다음과 같다.
- : Cell State Vector
- : Hidden State Vector
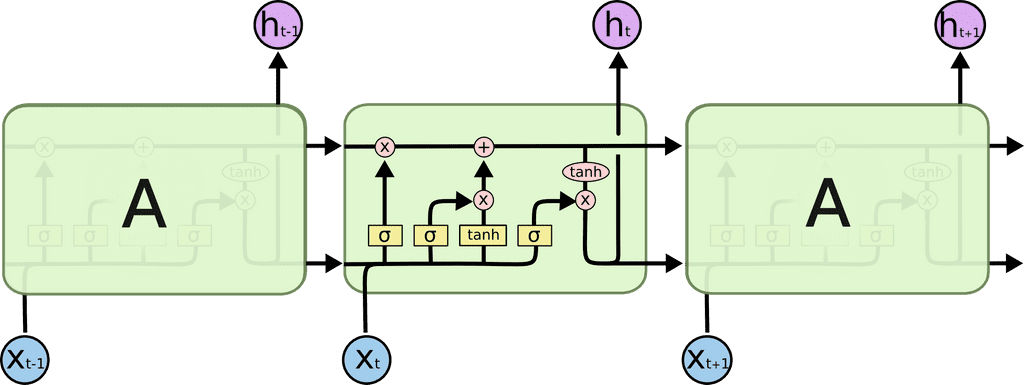
이 중 가 좀 더 완전하고 통합적인 정보를 제공한다. 는 를 한번 더 가공(필터링)해서 해당 timestep에서 노출할 필요가 있는 정보들만 남긴 형태라고 볼 수 있다.
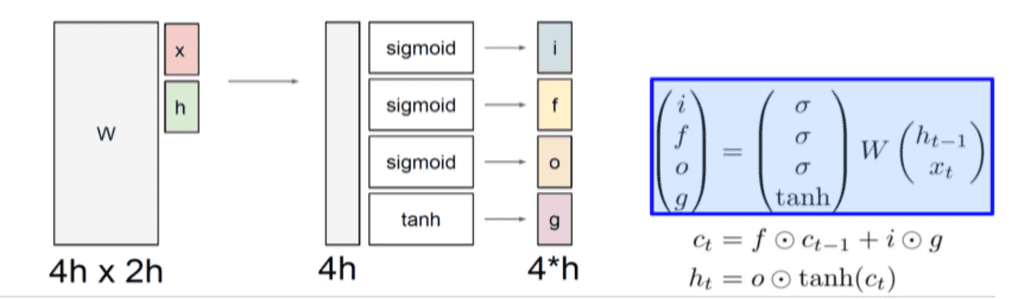
LSTM은 주어진 와 을 바탕으로 4개의 게이트(gate)를 이용해 를 수정하고 를 계산한다.
먼저, 와 을 붙여 를 이용하여 벡터로 선형변환시키고, 변환시킨 벡터를 4개로 쪼개어 각각 sigmoid와 tanh를 취해 4개의 게이트를 만든다.
i:Input gate, 셀에 해당 정보를 써 넣을 것인가?f:Forget gate, 셀에서 정보를 얼마나 잊을 것인가? 거꾸로 말하자면, 얼마나 보존할 것인가?o:Output gate, 현재 Cell()를 출력값 로 가공할 때 얼마나 필터링 할 것인가?는 sigmoid를 거치므로 0~1 사이의 값이 된다.
최종 출력값 는 tanh를 거친 에 0과 1사이의 적절한 와 element-wise product함으로써 Cell state 정보를 일정 비율로 작게 만들어(filtering) 내보내는 값이다.
- 는 이전까지의 모든 과거 정보를 담은 벡터, 는 해당 time step에서 예측값에 사용하기 위해 지금 당장 필요한 정보만을 (로부터) 필터링한 값이다.
g:Gate gate, 현재 cell에 해당 정보를 얼마나(how much) 기록할것인가?- 는 Gate gate 값이며, 현재 timestep에서 만들어진 정보를 의미한다.
- : 현재 정보를 기억할 게이트 값으로, Gate gate 값 이 Input gate 값 과 elemen-wise product된다.
- 이 때, Gate gate 값 은 tanh연산을 거쳤으므로 범위가 -1~1이다. 따라서, 를 Cell state에 반영시키되, 가 반영의 방향(증감)을 정한다고 볼 수 있다.
- 이후, 이전 Cell state가 forget gate 값 와 더해져 새로운 를 만든다.
sigmoid 사용 : i, f, o
- 0과 1 사이의 값을 가지는 sigmoid의 특성 상 기존의 벡터 값을 일정 부분만 떼내어 보존하는 역할을 한다.
tanh 사용 : g
- -1과 1 사이의 값을 가지는 tanh의 특성 상 현재 timestep에서 계산되는 유의미한 정보(증/감)를 담는 역할을 한다.(vanilla rnn에서의 마지막 tanh와 같음)
GRU
Gated Recurrent Unit(GRU)은 LSTM의 모델 구조를 경량화하여 메모리 요구량을 줄이고 빠른 학습이 가능하도록 만든 모델이다.
구조
기존의 LSTM이 와 를 이원화하여 가져가는 모델이었다면, GRU는 두 state vector를 합쳐 하나만 남겨놓았다. 이때, 일원화된 는 LSTM에서의 핵심적인 역할을 하던 Cell state vector 에 의미적으로 더 유사한 값이다.
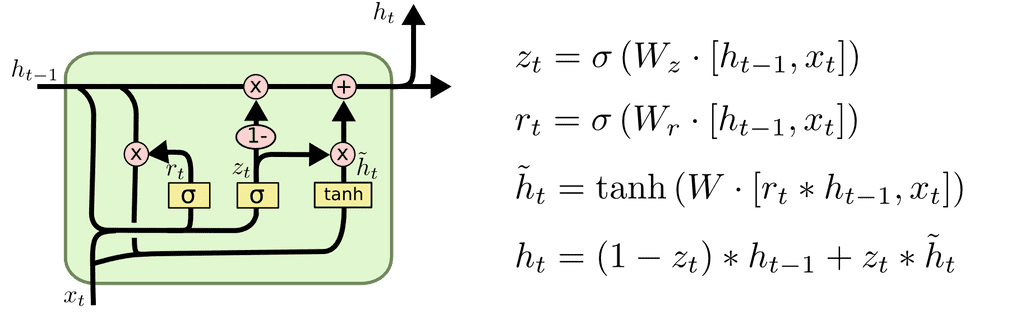
기존 LSTM에서는 input gate와 forget gate 값을 이용했다면, GRU에서는 input gate에 해당하는 만 남겨두고, forget gate 를 로 바꾸어 처리한다.
현재 값인 와 과거의 정보를 통합한 값인 의 비율을 조정하여, 합쳐서 1이 되도록 만들면서, 현재와 과거 값 간의 가중평균을 내게 된다.
- 이 과정에서 게이트도 하나(fortget gate) 줄이게 되어, 계산양과 메모리 요구량을 줄여 경량화하였다.
LSTM과 GRU의 역전파
기존의 RNN은 역전파 과정에서 를 계속 곱해주었기 때문에 Vanishing/Exploding Gradient 문제가 생겼었다.
그러나, LSTM(과 GRU)의 역전파는 Cell State Vector 에 그 때 그 때 다른 값으로 이루어지는 를 곱하고, 필요로 하는 정보 관련 항을 더해주어 Vanishing/Exploding Gradient를 막았다.
또한, 이러한 덧셈 연산이 역전파과정에서 Gradient를 복사하여 매번 전달해주는 역할을 하므로,, RNN에 비해 멀리있는 timestep의 gradient까지 큰 변형없이 전달하게 되어 결과적으로 long-term depandency를 어느정도 확보하였다. 다만, LSTM과 GRU는 Long Term Dependency 문제를 완벽하게 해결하지는 못했다. 멀리 있는 정보는 곱해져 최근으로 오면서 점점 소실되게 된다.
2017년 등장한 attention 구조를 활용한 transformer가 이러한 문제를 근본적으로 해결하게 되었다.
RNN/LSTM/GRU 요약
RNN은 다양한 길이를 가질 수 있는 시퀀스 데이터에 특화된 딥러닝 모델이다.- 아키텍쳐 디자인에 유연성을 제공한다.
Vanilla RNN은 구조가 간단하지만 Vanishing/Exploding Gradient 문제 때문에 실제로 많이 사용되지는 않는다.LSTM과GRU는 실제 많이 사용하고 있으며, Vanishing/Exploding Gradient 문제를 덧셈연산으로 해결한 모델이다.Cliping Gradient같은 방법으로 해결할 수도 있다고 한다.